Gradient Descent 연습
마침내 어제 저녁에 비던 시간 동안에 Gradient Descent를 구현할 수 있게 되었다. 근 몇 주 동안 대학의 수학 강좌에서 다변수함수의 Gradient와 편미분의 개념, 예전에 Machine Learning 강좌에서 주워 들었던 Gradient Descent에 대한 개념, 그리고 수치 미분에 관한 몇 가지 검색 정보를 활용했다.
Python의 matplotlib와 numpy를 이용했고, 다음과 같은 코드들로 아래의 이미지와 같은 결과를 얻을 수 있었다.
$f(x) = x^{2} \sin(x)$의 극소값 찾기 by Gradient Descent
import numpy as np
import matplotlib.pyplot as plt
import math
rate = 1e-2
x_in_gradient_descent = []
def diff(f, x):
h = 1e-4
return (f(x+h) - f(x-h)) / (2*h)
def gradientDescent(f, x):
x_in_gradient_descent.append(x)
if abs(rate * diff(f, x)) < 1e-8:
return (x, f(x))
next_x = x - rate * diff(f, x)
return gradientDescent(f, next_x)
def f(x):
return (x**2) * math.sin(x)
start = 0
end = 8
fig, ax = plt.subplots()
ax.set_xlim(start, end)
ax.plot(np.arange(start, end, 1e-4), [f(x) for x in np.arange(start, end, 1e-4)])
min_x, min_value = gradientDescent(f, 2.5)
y_in_gradient_descent = [f(x) for x in x_in_gradient_descent]
plt.plot(x_in_gradient_descent, y_in_gradient_descent, 'ro', markersize=1.5)
plt.title('Gradient Descent at $x^{2} \sin(x)$, start from $x=2.5$')
plt.show()
print(min_x, min_value)
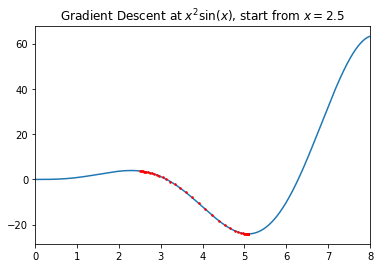
위 Gradient Descent의 결과로 $x \approx 5.087$에서 $-24.08$의 극솟값을 가짐을 확인할 수 있었다.
$f(x, y) = x^{4} + y^{4} – 4xy$의 극소값 찾기 by Gradient Descent
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
rate = 1e-3
cords = []
#이변수 함수의 각 편미분의 수치 미분 계산
def partial(f, var, x, y):
h = 1e-4
if var == 'x':
return (f(x+h, y) - f(x-h, y)) / (2*h)
elif var == 'y':
return (f(x, y+h) - f(x, y-h)) / (2*h)
pass
#이변수 함수의 Gradient 벡터 계산
def gradient(f, x, y):
return (partial(f, 'x', x, y), partial(f, 'y', x, y))
def gradientDescent(f, x, y):
cords.append((x, y))
if abs((rate * gradient(f, x, y)[0])) < 1e-4 and abs((rate * gradient(f, x, y)[1])) < 1e-4:
return x, y, f(x, y)
if not abs(rate * gradient(f, x, y)[0]) < 1e-4:
nx = x - rate * gradient(f, x, y)[0]
pass
else:
nx = x
pass
if not abs(rate * gradient(f, x, y)[1]) < 1e-4:
ny = y - rate * gradient(f, x, y)[1]
pass
else:
ny = y
pass
return gradientDescent(f, nx, ny)
def f(x, y):
return x**4 + y**4 - 4*x*y
# 그래프 그리기
div = 500
x = np.linspace(-5, 5, div)
y = np.linspace(-5, 5, div)
z = np.zeros((len(x), len(y)))
for i in range(div):
for j in range(div):
z[j, i] = f(x[i], y[j])
pass
pass
xx, yy = np.meshgrid(x, y)
plt.figure(1, figsize = (10, 10))
ax = plt.subplot(111, projection='3d')
ax.plot_surface(xx, yy, z, alpha=0.3, color='blue', edgecolor='gray')
# Gradient Descent from (start_x, start_y)
start_x = 4
start_y = 4
min_x, min_y, min_f = gradientDescent(f, start_x, start_y)
print(min_x, min_y, min_f)
ax.plot([x for x, y in cords], [y for x, y in cords], [f(x, y) for x, y in cords], 'ro', markersize=1.5)
plt.title('Gradient Descent at $x^4 + y^4 - 4xy$ start from (4,4)', pad=30)
plt.show()
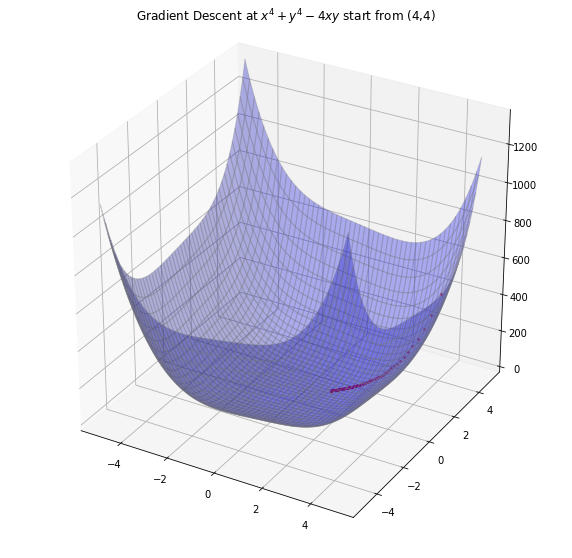
위 Gradient Descent의 결과로 $(x, y) \approx (1.012, 1.012)$에서 $-1.999$의 극솟값을 가짐을 확인할 수 있었다.