대기수치모델링 개론 및 실습 Final 대비

Aerosol Scheme

#1. Aerosol이 존재하는 위치에 따른 분류

Aerosol은 구름 입자 내에 존재하는지, 강수 입자 내에 존재하는지, 그냥 대기 중에 존재하는지에 따라 다음과 같이 세 종류로 분류된다.

1. Cloud-borne Aerosol: 구름 입자 안에 존재하는 Aerosol
2. Precipitation Aerosol: 강수 입자 안에 존재하는 Aerosol
3. Intertestial Aerosol: 대기 중에 그냥 존재하는 Aerosol

#2. Aerosol의 크기에 따른 분류

보통 많은 경우 Aerosol Scheme에서 Aerosol들은 그 입자 크기에 따라 다음 세 종류로 분류되는 편이다.

1. Aitkten mode: 가장 작은 Aerosol의 종류
2. Coarse mode: 중간 크기 Aerosol의 종류
3. Accumulation mode: 가장 큰 크기 Aerosol의 종류

#3. Aerosol의 Life Cycle

Aerosol은 지면에서 방출되거나, 대기 중 화학 반응에 의해 형성된다. Aerosol은 Dry Deposition (중력에 의해 대기 중 부유하는 Aerosol이 가라앉는 현상) 이나 Wet Deposition (강수에 Aerosol이 포집되어 가라앉는 현상. 이 현상은 Intertestial Aerosol이 Precipitation-borne Aerosol로 전환되는 과정으로 볼 수도 있다)으로 가라앉는다. 강수 입자가 증발하거나 Entrainment 등으로 구름 입자가 증발하는 경우, Cloud-borne Aerosol과 Precipitation-borne Aerosol이 Interstitial Aerosol로 전환될 수 있다. Aerosol은 CCN(Cloud Condensation Nucleri)로 작용하기 때문에, 핵화나 Activation 등와 과정에 연관되는 경우 Interstitial Aerosol에서 Cloud-borne Aerosol로 전환된다.

즉, Aerosol은 Cloud-borne, Precipitation-borne, Interstitial Aerosol 사이를 전환한다.

Aerosol Scheme은 이러한 Aerosol의 Emmision, Deposition, 전환 등을 모두 모사하는 Scheme이다.

#4. CAM5의 Aerosol Scheme

CAM5에서는 Aerosol Scheme으로 Modal Aerosol Scheme을 사용한다. Modal Aerosol Scheme은 Aerosol의 질량과 Number를 모두 고려하며, Dust, Sea Salt, Black Carbon, SOA, Surfate로 총 5종의 Aerosol을 다루며 Aitken mode, Coarse mode, Accumulation mode로 총 3종 크기의 Aerosol을 다룬다.

Modal Aerosol Scheme의 경우 Aerosol의 Emmision을 다룰 때, online과 offline, no의 3 모드를 나누어 생각한다. online의 경우는 Aerosol의 지표로부터의 방출량이 지표 부근의 유속에 비례한다고 setting한 경우이고, offline의 경우는 Aerosol의 지표로부터의 방출량이 유속과 무관하게 상수로 주어진다고 setting한 경우이다. no의 경우는 SOA와 같이 지표로부터 방출되는 것이 아니라, 지표로부터 방출된 Aerosol이 대기 중에서 화학 반응을 일으켜 새로이 형성되는 경우에 해당한다.

Radiation Scheme

#1. CAM5의 Radiation Scheme

CAM5에서는 RRTMG Radiation Scheme을 사용한다. Radiation Scheme은 대기의 각 layer를 여러 sub-column으로 나누어, 각 column에서의 cloud overlapping 수준(maximum overlapping, minimum overlapping, random overlapping 등)을 고려하여 복사 수지를 계산한다.

일반적으로 Radiation Scheme은 sub-column을 상당히 자잘하게 나누기 때문에, 연산량이 많아 속도가 매우 중요하다. RRTMG Radiation Scheme의 경우는 Monte Carlo 기법을 이용하여 연산량을 줄여 속도가 빠른 편이다.

Cloud Macrophysics & Cloud Microphysics Scheme

#1. Cloud에서 중요한 변수들

Cloud Macrophysics, Microphysics Scheme에서는 다음 5가지 변수를 주로 다룬다.

1. $a$: Cloud Fraction
2. LWC: Liquid Water Content
3. IWC: Ice Water Content
4. $N(i)$: Number Distribution of Ice Water Content
5. $N(l)$: Number Distribution of Liquid Water Content

#2. Cloud Macrophysics와 Cloud Mircophysics의 차이점

Cloud fraction, Vertical overlapping, Net Condensation Rate 등 전반적이고 거시적인 구름의 특성치들을 계산하는 Scheme을 Cloud Macrophysics라 한다. 반면, LWC, IWC의 양($q_l$, $q_i$)과 그 개수 분포, 크기 분포 등을 계산하여 강수를 계산하는 Scheme을 Cloud Microphysics라 한다.

Cloud Microphysics는 다루는 Hydrometer의 종류에 따라 3-Class, 5-Class, 6-Class로 나누기도 한다. 3-Class는 가장 주요한 Cloud liquid droplet, Water Vapor, precipitation을 다루고, 여기에 Snow와 Ice crystal을 추가한 것이 5-Class, Graupel (싸락눈) 을 추가한 것이 6-Class이다.

Cloud Microphysics의 경우 입자 반경에 따른 개수 분포 $N(D)$를 계산할 때 보통 Gamma 분포를 이용하는데, 이 때 Gamma 분포의 모수 $m$과 $q$, $N$ 등에 대하여 $q$만 계산하는 Microphysics Scheme을 Single-moment, $q$와 $N$을 모두 계산하는 Scheme을 Double-moment, 세 개를 모두 계산하는 Scheme을 Triple-moment라 한다. 보통 Triple-moment는 거의 개발되어 있지 않다.

Convection Scheme

#1. Convection Scheme은 무슨 일을 하는가?

대기 중에서 일어나는 Convection은 대체로 Assymetric Turbulent Flow이다. 마치 빨대를 이용해 물을 뽑아 올려 마시는 것처럼 좁은 상승 · 하강 흐름과 그 주변의 Compensating Substance 등이 있는 Assymetric한 Turbulence에 의하여 연직적으로 물리량 $\phi$가 어떻게 수송되는지 계산해주는 Scheme을 Convection Scheme이라 한다.

Symmetric하고 Local한 Turbulent에 의한 연직 물리량 수송을 고려했던 PBL Scheme과는 달리, Convection Scheme의 경우는 일반적으로 Mass Flux를 이용하여 연직 수송량을 계산한다.

#2. Mass Flux란? 그리고 이 Mass Flux를 이용하여 Convection Scheme에서는 연직 물리량 수송량을 어떻게 계산하는가?

단위 시간당 단위 면적을 통해 수송되는 공기의 질량을 Mass Flux라 한다. $\hat{M} = \rho \hat{a} (\hat{w} – \bar{w})$로 흔히 정의된다.

Convection Scheme에서 계산식은 다음 4가지를 이용한다.

1. $\bar{\phi\prime w\prime} = {{1} \over {\rho}} \hat{M} (\hat{\phi} – \bar{\phi})$
2. ${{1} \over {M}} {{\partial M} \over {\partial t}} = \hat{\epsilon} – \hat{\delta}$
3. ${{\partial \hat{\phi}} \over {\partial t}} = – \epsilon (\bar{\phi} – \hat{\phi}) + S$
4. ${{1} \over {2}} {{\partial {\hat{w}^2}} \over {\partial t}} = a B – b \epsilon \hat{w}^2$

#3. Convection Scheme에서 중요하게 다루어야 하는 Mesoscale Organized Flow에 대해 설명하시오.

Convection Cell에서는 entrainment 등에 의하여 공기가 유입되는 경우, 증발이 일어나 온도 하강, 밀도 증가로 convective downdraft가 발달할 수 있다. 또, convection에서 내리는 강수가 증발하여 온도가 하강할 수도 있다. 이 convective downdraft는 convection 아래쪽 지표 부근에 cold and dry한 cold pool을 형성한다.

인접한 Convection Cell에서 cold pool이 형성되어 전파될 때, 그 gust front가 충돌하는 경우 Mass conservation에 의하여 상승 기류가 발달할 수 있다. 이 상승 기류는 그 부근에서 새로운 convection을 형성하는데 기여한다. 이러한 흐름을 Mesoscale organized flow라 하며, 이 mesoscale organized flow를 잘 모의하는 것이 Convection Scheme에서 필요하다. 일반적으로 현재까지 학계에서 mesoscale organized flow는 잘 모의하지 못했지만, UNICON은 가능하다.

PBL Scheme

#1. PBL Scheme의 동작 원리에 대해 설명하시오.

PBL Scheme은 Local하고 Symmetric한 Turbulent에 의한 연직 물리량 수송을 계산하는 Scheme이다. Local한 경우, 즉 Turbulent의 연직 규모가 충분히 작아, 물리량의 연직 Flux를 Eddy Diffusivity와 local mean 물리량 gradient를 이용하여 계산할 수 있는 경우, 다음과 같이 계산한다. $\bar{w\prime \phi\prime} = K {{\partial \bar{\phi}} \over {\partial z}}$

이 때 Eddy Diffusivity의 경우는 Instability Function S와 연직 길이 interface간 간격 $l$, TKE(Turbulent Kinetic Energy) $e$에 대하여 $K = l \sqrt{e} S$로 계산된다.

PBL Scheme은 연직적으로 여러 layer를 나누어, 각 layer에서 사이의 interface에서 Richardson Number를 계산한다. Richard Number는 $Richardson Number = – {{BP} / {MP}}$로 정의되며, BP는 Buoyancy production, MP는 Shear Production이다. BP가 클수록, 그리고 Shear Production이 작을수록 대기가 불안정하므로, 해당 층에서의 대기 불안정도를 나타내는 Richardson Number는 값이 작을수록 대기가 불안정함을 나타낸다. 보통 Ri = 0.19 정도를 경계값으로 하며, Ri < 0 이면 대기가 불안정하다고 보고 CL(Convective Layer)라 하며, Ri가 0 ~ 0.19 사이이면 MP에 의하여 대기가 Turbulent하다고 보고 STL(Stably Turbulent Layer)라 한다. Ri가 0.19보다 크면 대기가 안정함을 지시한다.

PBL Scheme서 Boundary Layer Top 부근의 경우, 오직 Entrainment만이 일어나고 아래쪽에서 위쪽으로의 perturbation 흐름은 거의 없기 때문에, Eddy Diffusivity를 좀 다르게 계산한다. 이 경우 EI (Entrainment Interface)에서 Eddy Diffusivity $K = W_{e} \Delta z$로 계산한다.

#2. Moist Turbulence에서 공기를 냉각시킬 수 있는 과정은?

Moist turbulence가 있는 경우, entrainment에 의해 유입된 건조 공기에 의해 습윤한 공기에서 evaporation cooling이 일어나거나, rain evaporation에 의해 cooling이 일어나는 등의 과정을 통해 공기가 냉각될 수 있다.

또, PBL의 Top 구름에서는 LW Cooling이 강하게 일어남이 알려져 있다. 이 역시 공기를 냉각시키는데 크게 기여한다.

#3. BP, MP의 정의?

• BP (Buoyancy Production): $BP = {{g}\over{\theta_v}} \bar{w\prime\theta_{v}\prime}$
• MP (Shear Production): u, v의 연직 속력과의 perturbation 곱 평균에 각 방향 평균장 연직 gradient를 곱한 것, 즉 $MP = – \bar{w\prime u\prime} {{\partial \bar{u}}\over{\pratial z} – \bar{w\prime v\prime} {{\partial \bar{v}}\over{\pratial z}$

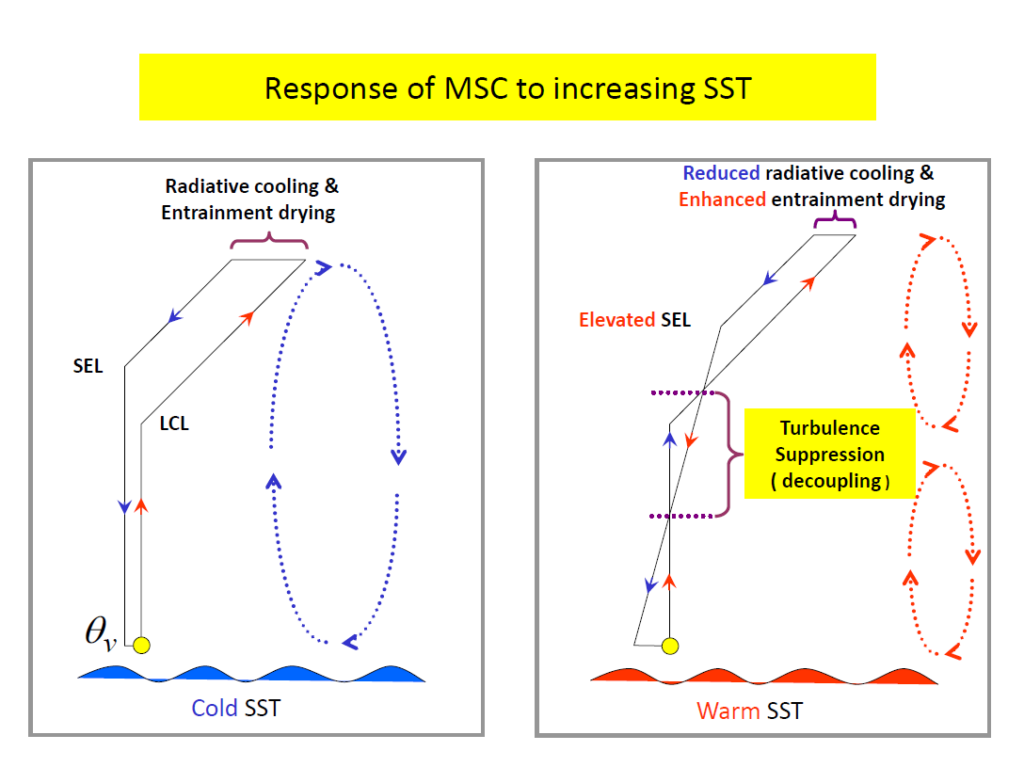
#4. PBL Decoupling이란?

높은 SST의 경우, PBL에서의 Convection이 두 개로 쪼개지는 현상을 PBL Decoupling이라 한다.

일반적으로 SST가 증가하는 경우, 두 가지 효과가 발생한다. 첫째. 전반적으로 PBL 하층의 온도가 증가하기 때문에 PBL Top에서의 역전층의 강도가 약해진다. 이 때문에 역전층을 뚫고 Entrainment가 더 잘 일어날 수 있고, Top에서의 LW Cooling이 약해진다.

표면서 SST에 의해 조금 높은 $\theta_v$는 공기가 단열 상승한다면 LCL에 도달할 때까지는 유지된다. 그러나 응결이 일어나기 시작하면 응결에 따른 잠열 방출로 인해 $\theta_v$는 증가하게 된다.

Boundary Layer Top에 도달하면 $\theta_v$는 Entrainment에 의한 Evaporation Cooling과 LW Cooling으로 인해 감소하게 되고, 이후 Dense해지기 때문에 다시 내려가게 된다. 이 때는 내려가면서 강수 증발이나 Evaporation Cooling의 영향으로 $\theta_v$가 점차 감소하다가, 일정 고도에 도달하여 모든 물방울이 증발하면 그때부터는 $\theta_v$가 보존된다. 다시 해표에 도달한 공기는 LHFLX와 SHFLX에 의해 가열되어 증가한다.

높은 SST의 경우 이러한 흐름을 따져보면, BP > 0인 지역이 상층과 하층의 2개 영역으로 쪼개지게 된다. 이 때문에 SST가 높아지면 PBL에서의 Convection이 2개로 쪼개지는 Decoupling 현상이 나타나는 것이다!

그 외 복습해야 하는 것들

• FVM, FDM, SEM Method
• Effeciency Factor의 정의 (해당 방법을 이용할 때 storage factor 개수 / 안정하게 적분 가능한 최대 적분 시간)
• Storage Factor의 정의 (해당 방법을 이용하여 다음 Timestep을 계산할 때 저장해야 하는 변수의 개수)
• 각 유한차분법에서(Forward, Backward, Trapezoidal (Central) Storage Factor, Efficiency Factor, Amplitude Error, Phase Error)
  • Forward: Amplifying, Phase 느려짐, 모델 잘 터짐, Storage Factor 2, Efficiency Factor 0, Explict Scheme
  • Backward: Damping, Phase 느려짐, 모델 좀 덜 터짐, Storage Factor 2, Efficiency Factor inf, Implict Scheme
  • Central: 오차 좀 덜함. Implict Scheme
• Mesh Refinement, Scalability
• Vertical Coordinates: z, P, Sigma-coord($\sigma = {{P – P_t}\over{\Pi}}$, 지형이 있어도 정의 잘 됨. 상층에서 좀 올라가는 문제 있음)