지적여정 #5. 태양상수의 유도

‘지적여정’ 시리즈는 필자가 고등학교 수업 시간에 떠올린 의문점 등에 대하여 자체적인 자료 조사나 연구를 통하여 그 답을 찾고, 기록해두기 위해 기획되었습니다.

질문

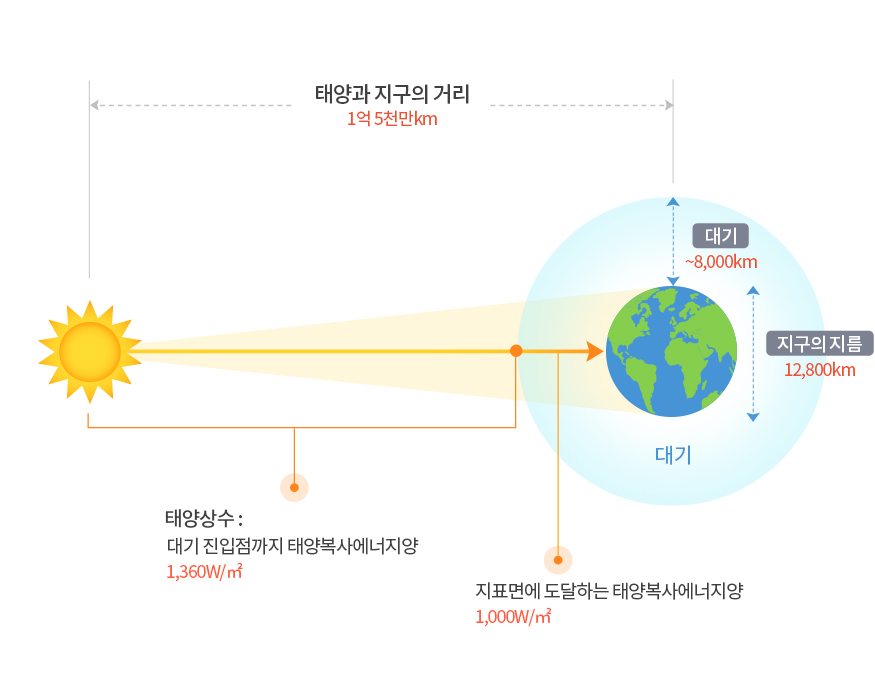
태양상수(지구에서 태양복사선에 수직인 단위 면적, 단위 시간당 받는 태양 복사 에너지)는 태양-지구 간의 거리를 1AU를 기준으로 할 때 평균값은 $1.36 \times 10^3 W/m^2$, 분당 받는 총 에너지는 약 $81.65kJ/m^2$이다. 어떻게 이러한 값이 유도된 것일까?

황수민 선생님. 고급지구과학 실험 <대기에서의 복사> 수업 중 떠오른 질문

대답

결과적으로 이러한 결과는 거의 흑체로 근사할 수 있는 태양이 시간당 표면에서 방출하는 복사 일률을 지구에서 받는 상황에 대해서 계산하여 얻어진 것이다.

태양 상수를 구하는 과정을 먼저 살펴보기에 앞서서 우선 슈테판-볼츠만 법칙을 알아 두는 것이 좋을 것 같아서 먼저 기술하겠다.

슈테판-볼츠만 법칙

주어지는 모든 파장의 전자기파를 흡수하는 가상의 물체를 흑체(Black Body)라고 한다. 흑체가 단위 시간, 단위 면적당 방출하는 에너지(단위 면적 당 일률)은 그 흑체의 표면 절대온도의 4승에 비례한다는 것을 슈테판-볼츠만 법칙이라고 한다.

${{dE} \over {A dt}} = \sigma T^4$, 슈테판-볼츠만 상수: $\sigma = 5.6696 \times 10^{-8} W/m^{2} K^{4}$

슈테판-볼츠만 법칙

태양 상수의 유도

태양의 경우는 흑체가 물론 아니긴 하지만 근사적으로 흑체로 취급할 수 있다. 태양이 그 표면적을 통하여 방출한 전자기 복사에 의한 일률은 당연히 지구가 그 표면 위에 있는 구의 표면적을 통과하는 일률과 동일하다. 이것을 이용하여 태양 상수를 유도하자.

먼저 필요한 물리량은 다음과 같다. 태양의 반지름의 경우는 대학물리학 Serway Vol.9 KOR 판을 참고하였는데, 뒤쪽 부록에 값이 잘못 적혀있었던 덕분에 10분을 허비했다. 저자들에게 너무 고마웠다.

태양의 일률: ${{dE_{sol}} \over {dt}} = A \sigma T_{sol}^{4} = (4 \pi R_{sol}^{2})(\sigma T_{sol}^{4})$

일률 동일: $(4 \pi R_{sol-earth}^{2})I = {{dE_{sol}} \over {dt}}$

$\therefore I = {{1} \over {4 \pi R_{sol-earth}^{2}}} {{dE} \over {dt}} = {{{4 \pi R_{sol}^{2}} \sigma T_{sol}^{4}} \over {4 \pi R_{sol-earth}^{2}}} = ({{R_{sol}} \over {R_{sol-earth}}})^{2}(\sigma T_{sol}^{4})$
$ = ({{6.96 \times 10^{8} m} \over {1.496 \times 10^{11} m}})^{2}(5.6696 \times 10^{-8} W/m^{2}K^{4})(5800K)^{4} = 1.39 \times 10^{3} W/m^{2})$

따라서 1분 동안의 지구의 단위 면적에 입사한 에너지는 $E = (1.39 \times 10^{3} W/m^{2})(60s) = 83.3kJ/m^{2} min$

이는 알려진 평균값과 약 2.2% 정도의 오차를 가지므로 받아들일 수 있는 값이다.