지적여정 #7. 온위와 푸아송 공식

‘지적여정’ 시리즈는 필자가 고등학교 수업 시간에 떠올린 의문점 등에 대하여 자체적인 자료 조사나 연구를 통하여 그 답을 찾고, 기록해두기 위해 기획되었습니다.

질문

온위는 무엇이고, 어떤 대기의 온위를 구하는 푸아송 방정식은 어떻게 유도된 것일까?

황수민 선생님. 고급지구과학 실험 <대기 열역학> 수업 중 떠오른 질문

대답

온위와 푸아송 방정식을 이해하기 위해서는 생각보다 알아야 할 배경 지식이 많다. 하나씩 살펴보도록 하자. 알아보아야 할 것이 좀 많이 긴 관계로 하여, 여기에 목차를 둔다.

1. 온위의 정의

2. 열역학 제1법칙

3. PV일(이상기체가 외부에 한 일)

4. 대기과학에서의 이상기체 상태 방정식

5. 연직 정역학적 압력 평형

6. 단열 감률과 단열 감률의 유도

7. 건조 단열 감률의 유도

8. 푸아송 방정식(온위 공식)의 유도

1. 온위의 정의

어떤 기층에 있는 공기덩어리를 건조 단열적으로 강제 상승, 또는 하강시켜서 1000hPa 기압고도까지 옮겼을 때의 기온을 그 공기의 온위라 한다. 이 때, 여기서 건조 단열 과정이라 함은, 수증기를 포함하지 않은 건조 공기가 대기 중에서 외부와 열 교환 없이(=단열적으로) 일어나는 변화를 말한다.

온위의 활용: 고도가 다른 공기 덩어리의 비교

그런데 이 온위를 도대체 어디다가 써먹을까? 그 질문에 대한 답은 온위가 등장한 배경에 있다.

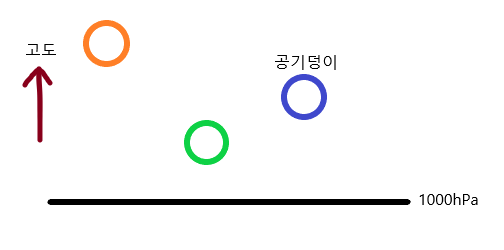
위 그림을 보자, 각기 다른 고도에 위치하고 있는 세 공기 덩어리들이 보인다. 만약 세 공기의 온도가 모두 같다면, 셋이 가진 내부에너지도 모두 같을까? 아니, 그렇지 않다. 각 공기는 고도가 다르기 때문에, 단열 과정을 따라 변화하는 공기 덩어리는 상승-하강 과정을 통해서 공기 덩어리가 외부에 일을 할 수도 있고 외부에서 일을 받을 수도 있기 때문에, 열역학 제1법칙을 생각해보면 공기의 온도는 고도에 따라 달라질 수밖에 없다. (이 부분이 이해되지 않는다면 아래쪽 열역학 제1법칙, PV일을 먼저 읽고 오기 바란다)

그러면 이 공기 덩어리들을 어떻게 비교해볼 수 있을까? 그 대답은 공기 덩어리를 어떤 기준이 되는 ‘같은 고도’로 옮겨서 비교하는 것이다. 그러면 공기 덩어리를 고도에 따른 온도 변화를 고려하지 않고도 공정하게 비교할 수 있을 것이다.

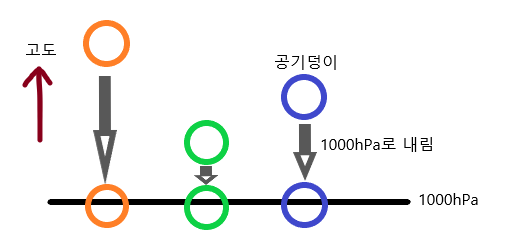
온위는 이처럼 서로 다른 고도에 위치하고 있는 공기들의 상태와 특성을 비교하기 위한 개념으로 등장하였다. 즉, 각 공기덩어리들을 ‘같은 고도’로 옮겨서 비교하려는 시도로부터 유래한 셈이다.

이런 유래를 가지고 있는 온위이므로, 그 활용법 중 하나는 ‘서로 다른 고도에 위치한 공기 덩어리의 비교’라는 것을 알 수 있다. 하지만, 또 다른 온위의 활용법이 하나 더 있다.

온위의 활용: 대기 안정도

또 한 가지의 온위의 활용법은 ‘대기 안정도 판별’이다. 하지만 먼저, 한 가지 전제를 기억하도록 하자. 온위의 정의를 생각하자. 그 정의는, ‘건조 단열 과정’하에 공기 덩이를 1000hPa 기압고도로 이동시킬 때의 공기의 온도이다. 따라서, 건조 단열 과정을 따라 이동한 공기의 경우는 온위가 보존된다.

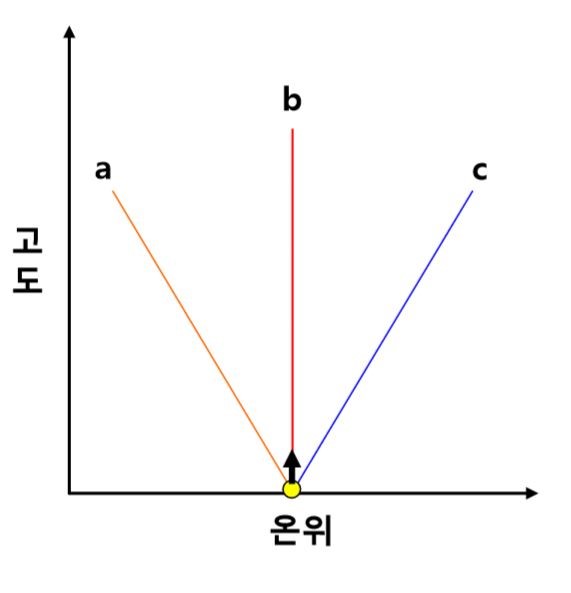
상기 도식은 각각 불안정, 중립, 안정한 대기에서의 고도에 따른 온위의 변화를 나타낸 것이다. (고도에 따른 온위 변화란, 지표를 기준으로 해서 각 고도의 공기의 온위를 도식한 것이다 / 만약 불안정, 중립, 안정 대기의 용어를 이해하지 못했다면, 구글링을 통해 ‘대기의 안정도’를 검색하여 관련 내용을 공부하기 바란다) 이제 각각 불안정, 중립, 안정 대기에서의 고도에 따른 온위 변화가 왜 저런 식으로 나타나는지를 이해해보도록 하자.

먼저, 불포화된 공기가 건조 단열적으로 상승하는 경우, 공기 덩이의 온위는 위의 도식에서 b: 중립선을 따라 움직이게 된다. 이 점에는 동의할 수 있을 것이다. 그러면, 주변의 환경 온위선(실제 대기의 고도에 따른 온위를 도식한 선)이 어떠느냐에 따라 대기 안정도를 판별할 수 있는데, 이는 공기 덩이를 움직여 대기 안정도를 판별한 기존의 방법과 동일하므로 익숙할 것이다.

먼저, 환경 온위선이 a: 불안정 선과 같이 고도에 따라 감소하는 경우를 생각해보도록 하자. 건조 단열을 따라 상승하는 공기의 온위는 b와 같이 수직선을 따라 일정한 모습을 보이기 때문에, 당연히 주변 공기보다 온위가 항상 높게 된다. 주변 공기보다 온위가 높다 함은, 실제 주변 공기와 상승하는 공기를 1000hPa로 건조 단열적으로 옮겼을 때 기온이 상승하는 공기가 높음을 지시한다. 건조 단열 감률은 모든 건조 공기에 동일하게 적용되므로, 따라서 해당 고도에서도 상승하는 공기의 온도가 주변 공기보다 높다는 것을 알 수 있다. 따라서, 상승하는 공기는 계속 상승하게 된다. 즉, 이 대기는 불안정하다.

다음으로, 환경 온위선이 c: 안정 선과 같이 고도에 따라 증가하는 경우를 생각해보도록 하자. 건조 단열을 따라 상승하는 공기의 온위는 역시 b와 같이 수직선을 따라 일정한 모습을 보이므로, 당연히 주변 공기보다 온위는 항상 낮게 된다. 마찬가지로, 주변 공기보다 온위가 낮다 함은, 실제 주변 공기와 상승하는 공기를 1000hPa로 건조 단열적으로 옮겼을 때 기온이 상승하는 공기가 낮음을 지시한다. 건조 단열 감률은 모든 건조 공기에 동일하게 적용되므로, 따라서 해당 고도에서도 상승하는 공기의 온도가 주변 공기보다 낮다는 것을 알 수 있다. 따라서, 상승하는 공기는 계속 상승할 수 없고, 다시 원래의 자리로 돌아오려는 움직임을 보인다. 즉, 이 대기는 안정하다.

마지막으로, 환경 온위선이 b: 중립 선과 같이 고도에 따라 일정한 경우를 생각해보도록 하자. 만약 환경 온위선이 수직선이라면 위의 논의과정으로 하여 모든 고도에서 상승하는 공기와 주변 공기의 온도가 일치함을 알 수 있다. 이는 곧 상승하는 공기가 자유롭게 상승 또는 하강하고, 별도의 특별한 강제적 경향성을 보이지 않는다는 것을 지시하므로, 이 대기는 중립임을 보여준다.

결과적으로, 다음의 결론을 내릴 수 있다.

1. 고도에 따라 환경 온위가 감소하면 이 대기는 (건조 대기에 대하여) 불안정하다.

2. 고도에 따라 환경 온위가 증가하면 이 대기는 (건조 대기에 대하여) 안정하다.

3. 고도에 따라 환경 온위가 일정하면 이 대기는 (건조 대기에 대하여) 중립 상태이다.

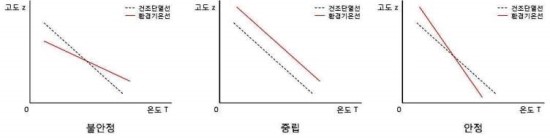
위 온위에 따른 대기 안정도 판별은 중고등학교 교과 시간에 학습하는 정적 안정도 판별(기온 감률을 이용한 대기 안정도 판별)에서, 고도에 따른 기온의 도식을 오른쪽으로 45도 돌린 것과 같다. 위 온위로의 대기 안정도 판별이 헷갈린다면, 왼쪽으로 45도 돌려 정적 안정도 판별의 방식대로 생각해도 된다는 말이다. (적어도 문제를 풀 때 만큼은, 자연현상은 실제 과정과 원리를 이해하는 것이 대단히 중요하다는 사실을 잊어서는 안된다!)

2. 열역학 제1법칙

물리학 수업을 들어본 사람이라면 이 법칙을 안 들어볼 수가 없을 것이다. ‘열물리’에서는 열역학에 관한 3가지 법칙을 배우는데(열역학 제0법칙까지 포함한다면 물론 4가지가 되기는 한다), 그 첫번째에 해당하는 법칙이 바로 이것이다.

하지만 흔히 배우기는 하지만 이 열역학 제1법칙을 잘못 이해하는 경우가 많다. 고립계에서의 에너지 보존 법칙으로 이해되는 경우가 많은데, 사실은 이 고립계가 특별한 형태의 고립계라는 사실을 망각하는 경우가 매우 많다. (고립계, 열린계, 닫힌계라는 용어를 이해하고 있지 않다면 빨리 구글링해서 공부하고 오길 바란다)

Serway 대학물리학 제9판의 설명에 따르면, 열역학 제1법칙은 보편적인 고립계에서의 에너지 보존 법칙이 아니며, 오히려 닫힌계이며 에너지 출입이 열과 일의 형태로 한정되는 특별한 형태의 계에 대한 에너지 보존 법칙으로 이해해야 한다.

가볍게 설명하도록 하자. 에너지 보존을 이해하고 있다면 이해가 되지 않을 수는 없을 것이다.

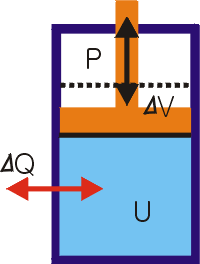
위 그림과 같은 닫힌 이상기체계를 고려하자. 계의 경계에서 열의 형태로 Q의 열량이 출입하고(이 때 Q의 부호: 계로 유입되는 방향을 (+), 계로부터 유출되는 방향을 (-)로 둔다), 계의 경계에서 PV일로(PV일은 다음 단락에서 자세히 설명할 것이다) W의 일이 출입한다면(W의 부호: 계가 주변에 일을 하는 방향이 (+), 계가 주변으로부터 일을 받는 방향이 (-)), 이 때 계의 내부에너지 변화(혹시나 하는 말인데, 계의 내부에너지와 열에너지가 헷갈리는 사람도 빨리 구글링해서 공부하고 오길 바란다. ‘계의 열에너지가 많다’라고 말하는 것은 완전히 틀렸으니, 이에 동의할 수 없는 이들은 빨리 공부하고 오길 바란다) $\Delta E_{int}$ 사이에는 다음의 수식적 관계가 성립한다는 것이 ‘열역학 제1법칙’이다.

$Q = {\Delta E_{int}} + W$

미분형: $dQ = dE_{int} + dW$

3. PV일

어떤 기체 계는 그 부피가 팽창하면 그 과정 중에 주위로 힘을 작용하여 주위를 밀어내므로, 외부로 일을 하게 된다. 반대로, 그 부피가 수축하면 그 과정 중에 주위에서 힘을 받게 되므로, 외부로부터 일을 받게 된다.

이상 기체계에서 기체의 압력(일에서 ‘힘’의 항과 관련된다)과 기체의 부피에 관련된 일의 출입을 PV일이라 한다.

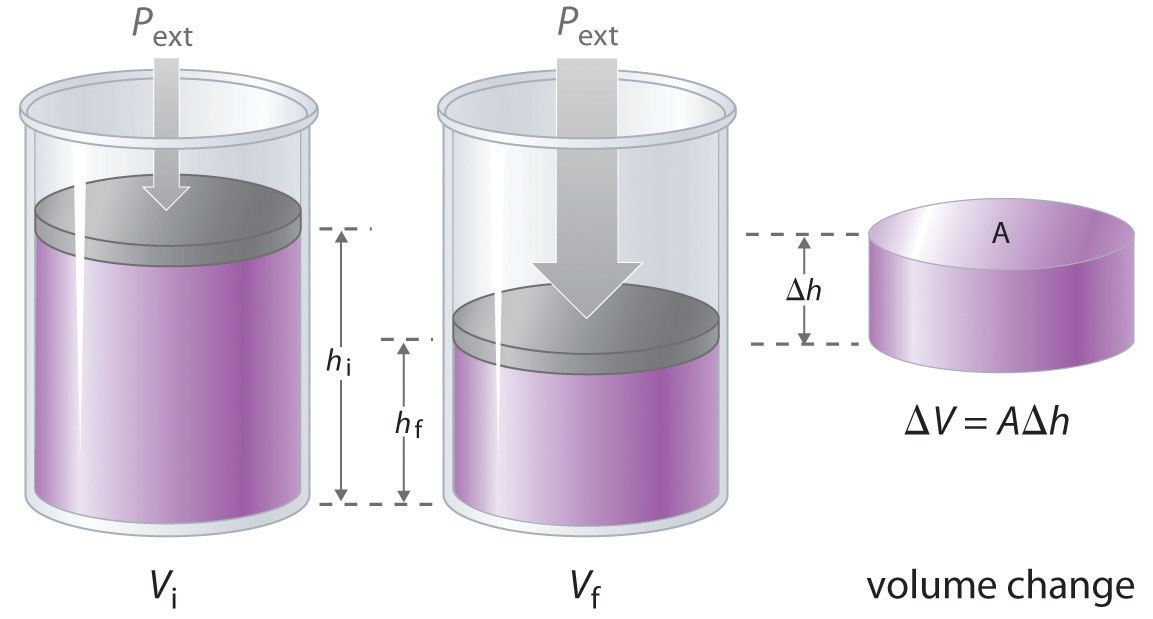
위쪽 그림과 같이 어떤 실린더에 담긴 이상 기체계가 매 순간 외부 압력 $P$와 균형을 이루면서(준정적으로) 등압팽창 또는 등압수축하여 부피 변화 $\Delta V$가 일어났다고 하자. 일의 부호를 기체가 외부에 일을 한 경우를 (+)로 한다고 하면, 어떤 기체가 외부 압력 $P$와 같은 내부 압력을 실린더에 작용하여 부피 $dV$만큼 팽창하였을 때, 기체가 외부에 한 일의 양 $dW$는,

$dW = Fdx = (PA)dx = P(Adx) = PdV$

따라서, 이 이상기체의 PV일은 다음과 같다.

미분형: $dW = PdV$

적분형: $W = \int_{i}^{f} {PdV}$

4. 대기과학에서의 이상기체 상태 방정식

화학에서 ‘이상기체’를 공부한 사람이라면 한 번은 들어보았을 ‘그 방정식’인 이상기체 방정식은, 역시 많이 들어보았을 보일의 법칙, 샤를의 법칙, 게이-뤼삭의 법칙, 아보가드로의 법칙을 종합하여 얻어진 결과이다.

보일의 법칙: 기체의 몰 수, 온도가 일정할 때, 기체의 부피 $V$는 기체의 압력 $P$에 반비례한다.

샤를의 법칙: 기체의 압력, 몰 수가 일정할 때, 기체의 부피 $V$는 기체의 절대온도 $T$에 비례한다.

게이-뤼삭의 법칙: 기체의 부피, 몰 수가 일정할 때, 기체의 압력 $P$는 기체의 절대온도 $T$에 비례한다.

아보가드로의 법칙: 기체의 압력, 온도가 일정할 때, 기체의 부피 $V$는 기체의 몰 수 $n$에 비례한다.

이상의 결과를 종합하면 화학에서의 몇 몰의 기체에 대한 다음의 이상기체 상태 방정식을 얻을 수 있다.

$PV = nR^{*}T$

(이 때, $R^{*}$은 흔히 ‘기체 상수’로 알고 있는 ‘보편 기체 상수’로, 일반적인 이상 기체 1mol에 대한 이상 기체 상태 방정식에서의 비례상수에 해당한다)

한 편, 이러한 이상 기체 상태 방정식은 mol 수를 기준으로 한 방정식이다. 대기과학에서는 질량을 기준으로 한 이상 기체 상태 방정식을 사용하는데, 이는 기체의 몰 수와 질량 사이의 다음의 관계를 이용하여 유도할 수 있다.

$n = {m \over M_{w}}$ … 어떤 기체의 몰 수는 그 기체의 총 질량을 분자량으로 나눈 값이다.

(이 때, $M_{w}$는 기체의 분자량이다)

이를 화학에서의 이상기체 상태 방정식에 적용하도록 하자.

$PV = nR^{*}T = {m \over M_{w}}R^{*}T = m{R^{*} \over M_{w}}T$

이 때, 기체 분자량에 대한 보편 기체 상수의 비율을 그 기체에 대한 ‘기체 상수'(이하 기체 상수) $R$로 정의하면,

$PV = mRT$

($m$은 기체의 질량, $R$은 기체 상수로 $R = {R^{*} \over M_{w}}$)

이 때, 단위 부피 당 질량에 해당하는, 밀도의 역수를 비적이라 정의하고, 기호로 $\alpha$로 쓰면, 다음의 정의식이 성립한다.

$\alpha = {V \over m}$

이를 위 질량 기준 이상기체 상태 방정식에 적용하여 정리하면, 다음과 같은 대기과학에서의 이상기체 상태 방정식을 얻을 수 있다.

$P{V \over m} = RT$

$P \alpha = RT$ (비적 $\alpha$)

$P = \rho RT$ (대기 밀도 $\rho$)

5. 연직 정역학적 압력 평형

어떤 균일한 중력장 $g$가 연직 하방으로 작용하는 공간 상에서, 유체 내의 한 부분이 어떤 위치에 정지해있다고 하자.

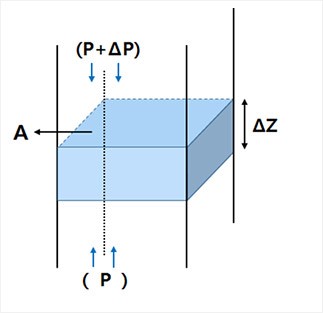
위쪽 그림과 같이 유체 내에서 단면적 $A$인 유체 기둥이 윗면에서 압력 $P$, 아랫쪽에서 압력 $P + \Delta P$를 받고 있고, 연직 하방으로 $mg = \rho Vg$의 중력을 받고 있다면 운동방정식에서:

$\sum {F_{y}} = (P + \Delta P)A – PA – \rho gA \Delta h = 0$

$\therefore \Delta P = \rho g \Delta h$

$\Delta P = \rho g \Delta h$

연직 정역학적 압력차.

6. 단열 감률의 유도

단열 감률, 건조단열감률과 습윤단열감률

높은 산에 올라가본 경험이 있다면, 주변 기온이 점차 낮아지는 것을 느낄 수 있었을 것이다. 이러한 현상은 ‘단열 감률‘이라는 기상학적 개념과 관련되어 있다.

단열 감률이란, 어떤 공기가 단열 과정을 따라 강제 상승하거나 하강할 때, 고도 변화에 대한 기온 변화의 비율이다.

일반적으로 HIGHTOP 지구과학 II의 내용에 따르면, 단열 감률에는 크게 2가지 종류가 있다. 첫째는 건조한 대기(불포화된 대기)에 대한 단열 감률인 건조단열감률이고, 둘째는 습윤한 대기(포화된 대기)에 대한 단열 감률인 습윤단열감률이다. (만약 불포화, 포화의 개념을 알고 있지 않다면 구글링을 통해 대기과학에서의 불포화 공기, 포화 공기, 과포화 공기와 이슬점 등의 개념을 학습하고 와 주기를 바란다)

건조단열감률과 습윤단열감률은 다음과 같다:

건조단열감률: 약 1℃ / 100m

습윤단열감률: 약 0.5℃ / 100m

건조단열감률보다 습윤단열감률이 더 작다는 사실을 발견했을 것이다. 그 이유는 실제로는 복잡하지만, 가장 간단하게 설명하자면 수증기로 포화된 대기의 경우, 단열압축 또는 팽창하면서 수증기가 물로 응결되거나 물이 수증기로 기화되기 때문에 이 과정에서 잠열(액화열 / 기화열)의 출입이 발생하기 때문이다.

여기에서는 단열감률과 건조단열감률만을 유도한다. 습윤단열감률의 경우, 공기의 습도에 따라 유도가 달라져 일정한 기준을 필요로 하는데, 필자의 수준에서 그 기준을 찾을 수가 없어 이들만의 유도를 보이겠다. 과정이 꽤 기므로, 마음의 준비를 미리 하도록 하자. (사실 대부분의 대기과학 서적에는 이들 과정이 생략된 경우가 더럽게 많다: 필자도 이것 때문에 꽤나 이 논리 전개를 모으고 병합하느라고 고생을 꽤나 했다)

단열 감률의 유도

어떤 질량이 $m$인 기체 덩어리가 건조 단열적으로 상승하는 상황을 생각해보자. 이 기체 덩어리는 이상기체로 가정할 수 있으므로, 변화 과정 내내 이 기체 덩어리는 다음의 (대기과학에서의) 이상기체 상태 방정식을 만족한다고 생각할 수 있다. (대기과학에서의 이상기체 상태 방정식의 유도가 이해되지 않았다면 앞선 절로 가서 살펴보고 오길 바란다)

$P \alpha = RT$

(기체의 비적 $\alpha$)

열역학 제1법칙에 따르면, 이 기체가 일련의 열역학적 과정을 겪을 때, 외부에서 기체로 전달된 열(방향에 유의해야 한다) $Q$, 기체 내부 에너지 변화량 $\Delta E_{int}$, 기체가 외부에 한 일(역시 방향에 유의) $W$에 대하여, 다음의 수식적 관계가 성립한다.

$Q = \Delta E_{int} + W$

이를 미분형으로 쓰면 다음과 같다.

$dQ = dE_{int} + dW$

대기과학에서는 질량 위주의 기술로 논의하고 있음을 기억하자. 편의를 위하여, 지금부터는 단위 질량(=1kg의 기체)에 대하여 논의하기로 하자. 위 미분형 열역학 제1법칙을 단위 질량의 기체에 대하여 기술한 형태(양변을 기체의 질량 $m$으로 나눈 것)를 다음과 같이 약속하도록 하자.

$dq = du + dw$ … (1)

(이 때 $q$는 단위 질량의 기체에 유입된 열, $u$는 단위 질량의 기체의 내부에너지 변화, $w$는 단위 질량의 기체가 외부에 행한 일)

이상기체의 PV일에 관한 앞선 고찰을 참고해보면, $dW = PdV$가 됨을 기억하자. 제시된 상황은 $m = 1kg$인 상황이므로, 따라서 부피 $V$가 지시하는 바는 비적 $\alpha$에 해당한다. 따라서, 단위 질량의 기체가 외부에 행한 PV일 $dw$에 대하여, 다음이 성립한다:

$dw = P d \alpha$

앞서 논의한 대기과학의 이상기체 상태 방정식에서 양변을 전미분하면,

$(P \alpha)’ = (RT)’$ $(R = {R^{*} \over M_{w}})$

$dP \alpha + Pd \alpha = RdT$

따라서, 어떤 단위 질량의 기체가 외부에 행한 일은 다음으로 정리할 수 있다.

$dw = RdT – dP \alpha$ … (2)

한 편, 어떤 이상 기체의 내부 에너지 변화량은 등적과정의 경우를 생각해보면, 등적과정을 따라 변화하는 이상 기체의 경우, 외부에 일을 하지 않으므로(PV일 없음) 그 때 기체계에 전달되는 열은 오직 계의 내부 에너지 변화만을 일으키게 된다(열역학 제1법칙). 이러한 논의는 등적과정이 아닌 경우에도 동일하게 적용되기 때문에, 어떤 이상기체계의 온도 변화에 의한 이상기체계의 내부 에너지 변화량은 미분형으로 다음과 같이 기술될 수 있다(이상의 논의를 이해하지 못했다면 등적과정과 내부 에너지 등, 열역학의 용어를 공부하고 오길 바란다).

$dE_{int} = nc_{v}^{*}dT$ (기체의 정적 몰비열 $c_{v}^{*}$)

아까부터, 우리는 단위 질량의 공기에 대하여 논의하고 있음을 기억하자. 역시, 우리는 이 수식을 단위 질량에 대한 상황으로 변환해야 한다. 앞선 몰 수의 정의로부터 우리는 위 수식을 다음과 같이 변형할 수 있다.

$dE_{int} = {{m} \over {M_{w}}}c_{v}^{*}dT$

역시 단위 질량의 기체에 대해 논의하고 있으므로, 양변을 기체의 질량 $m$으로 나누어 위 식을 다음의 형태로 정리할 수 있다.

$du = {{c_{v}^{*}} \over {M_{w}}}dT$

이 때 위 수식에서 기체의 평균분자량에 대한 정적몰비열은 결국 단위 질량의 기체를 등압과정에서 1K 올리는데 필요한 열(즉, 일반적인 비열)로써, 이를 $c_{v}$라 쓰기로 약속하자. 그러면:

$du = c_{v}dT$ … (3)

이상의 논의에서 등장한 (1), (2), (3) 식에 대하여, (2)와 (3)의 식을 (1) 식에 대입하여 정리하자.

$dq = du + dw$ … (1)

$dw = RdT – dP \alpha$ … (2)

$du = c_{v}dT$ … (3)

$\therefore dq = c_{v}dT + RdT – dP \alpha$

$\therefore dq = (c_{v} + R)dT – dP \alpha$

어떤 이상 기체의 정압몰비열 $c_{p}^{*}$와 정적몰비열 $c_{v}^{*}$에 대하여, 다음의 관계가 성립함은 물리에서 배웠다. (이것을 모르는 사람은 이상기체의 물리학적, 또는 열역학적 분석에 대하여 공부하고 오길 바란다)

${c_p^*} = {c_v^*} + {R^*}$ (보편기체상수 $R^{*}$)

마찬가지로, 단위 질량의 이상 기체에 대하여, 어떤 기체의 정압비열 $c_p$와 정적비열 $c_v$에 대하여, 다음의 관계가 성립한다.

$c_{p} = {{c_{p}^{*}} \over {M_{w}}}$

$c_{v} = {{c_{v}^{*}} \over {M_{w}}}$

$R = {{R^*} \over {M_w}}$

${c_p^*} = {c_v^*} + {R^*}$

$\therefore c_{p} = c_{v} + R$

따라서 최종적으로, 단위 질량의 기체에 대한 열역학 제1법칙의 수식(대기역학에서의 열역학 제1법칙의 정리형)은 다음과 같이 정리된다.

$dq = c_{p}dT – dP \alpha$

이 기체 덩어리가 건조 단열적으로 고도 $\Delta h$만큼 상승하는 상황을 생각하여, 이 기체 덩어리의 단열 감률을 계산해보도록 하자.

기체 덩어리는 주변과 열교환을 할 시간이 부족하므로, 이 과정은 근사적으로 단열 과정으로 볼 수 있다. 따라서 위 대기과학에서의 열역학 제1법칙의 정리형에서 $dq = 0$인 상황에 해당하며, 이는 다음과 같이 기술된다.

$c_{p}dT = dP \alpha$ … (4)

연직 정역학적 압력 평형을 생각해보자. 만약 이 기체 덩어리가 상승하는 모든 고도에서 연직 정역학적 압력 평형 공식에 의하여 도출되는 외부 압력에 노출되며 상승한다면, 정역학적 압력 평형 공식의 미분형에서:

$dP = \rho g dz$ ($\rho$는 기체의 밀도, $g$는 중력가속도) … (5)

(4), (5)에 의하여:

$c_{p}dT = \rho g dz \alpha$

${{dT} \over {dz}} = {{\rho g} \over {c_p}} \alpha = {g \over c_p}$ (비적 $\alpha$는 밀도 $\rho$의 역수)

따라서, 단열 감률 ${dT} \over {dz}$에 대하여:

${{dT} \over {dz}} = {g \over {c_p}}$ ($c_p$는 그 기체의 정압비열, 단위: J/kg K)

대기과학에서, 단열 감률.

건조단열감률의 유도

본격적인 수식적 유도에 들어가기 전에, 우선 대기과학에서 이 계산에 사용되는 근사를 하나 살펴보도록 하자.

지구의 대기의 조성이 어떤지 다들 중학교나 고등학교 수업 시간에 배웠을 것이다. 지구의 대기 조성을 살펴보면, 지구 대기는 위쪽 도표와 같이 거의 대부분(99% 이상)이 질소($N_2$) 기체와 산소($O_2$) 기체로 구성되어 있다. 이산화탄소($CO_2$), 아르곤($Ar$), 수증기($H_{2}O$)와 같은 기체들은 그 비율이 1% 이하로 매우 작다.

대기과학에서는 계산의 편의를 위하여, 다루는 기체를 저온 상태의 이원자분자 이상기체로 근사한다.

이 근사가 사용되는 이유를 위의 대기 조성에서 찾을 수 있다. 조성을 보면 거의 대부분의 대기가 이원자분자인 산소와 질소 기체로 이루어져 있다는 것을 발견할 수 있다. 대기 중 기상현상의 원인이 되는 수증기의 양도 극히 미미하므로, 따라서 대기과학에서는 거의 모든 계산에(실제 값을 뽑아내는) 위 근사가 사용된다.

이 저온 상태의 이원자분자 이상기체로의 근사를 기억하고, 다음의 수식적인 건조단열감률의 유도 과정을 살펴보도록 하자.

건조단열감률은 앞서 유도하였던 단열 감률의 수식과 공기의 평균 분자량을 이용해 계산할 수 있는 건조 공기의 정압비열을 이용하면 계산이 가능하다.

우선 건조 공기의 정압비열부터 계산하자. 건조 공기의 평균 분자량은 약 28.966 g/mol인데, 정압몰비열과 정압비열, 저온 상태의 이원자분자 이상 기체에서의 정압몰비열을 생각하면(이 부분을 이해하기 위해서는 반드시 물리학에서의 열역학 단원을 공부해야 한다!):

$c_{p}^{*} = {7 \over 2}R^{*}$

(저온 이원자분자 이상기체의 정압몰비열 $c_{p}^{*}$, 보편기체상수 $R^*$)

따라서 건조 공기의 정압비열 $c_{p, d}$:

$c_{p, d} = {{c_{p}^{*}} \over {M_w}} = {7 \over 2}{{R^*} \over {M_w}} = {{(7)(8.314 J/mol K)} \over {(2)(28.966 \times 10^{-3} kg/mol)}} = 1004.59 J/kg K$

$\therefore c_{p, d} = 1004.59 J/kg K$

건조 공기의 정압비열.

단열 감률의 수식으로부터:

${{dT} \over {dz}} = {g \over {c_p}}$ ($c_p$는 그 기체의 정압비열, 단위: J/kg K)

따라서 건조 기체에 대한 단열 감률에 해당하는 건조단열감률은:

${{dT} \over {dz}} = {{g} \over {c_p, d}} = {{9.80665 m/s^2} \over {1004.59 J/kg K}} = 9.7618 \times 10^{-3} K/m = 9.7618 ℃/km$

건조 기체에 대한 단열 감률에 해당하는 건조단열감률(Dry adabatic lapes rate)은 기호로 $\Gamma_{d}$로 표현한다.

$\Gamma_{d} = 9.7618 ℃/m$

건조단열감률.

이는 HIGHTOP 등, 고등학교 수준의 지구과학 교과서에서 일반적으로 제시되는 건조단열감률인 1℃/100m와 유사한 수치이다.

7. 푸아송 방정식(온위 공식)의 유도

푸아송 방정식은 단위 질량(1kg)의 공기에 대하여, 대기과학에서의 이상기체 상태방정식과 열역학 제1법칙, 단열 과정의 기술을 적용하여 얻은 것이다. 이하의 유도에서, 모든 논의는 단위 질량(1kg)의 공기에 대한 논의이다.

단열 감률의 유도 과정에서 대기 역학에서의 열역학 제1법칙은 다음의 변형된 형태로 기술될 수 있음을 보였다.

$dq = c_{p}dT – \alpha dp$

온위는 어떤 고도, 어떤 온도의 기체를 건조단열과정을 통해(또는, 단열선도에서 건조단열선을 따라 움직여) 1000hPa 기압고도로 옮겼을 때 기체의 온도이다. 건조단열과정은 단열과정이므로, 위 열역학 제1법칙의 정리형에 단열과정을 적용하면:

$c_{p}dT = \alpha dT$ … (6)

이 때, 대기과학에서의 이상기체 상태방정식으로부터:

$p \alpha = RT$, $\alpha = {{RT} \over {p}}$

이므로, 이를 (6)에 적용하면:

$c_{p}dT = RT{{dp} \over p}$ … (7)

(7) 식은 어떤 기체의 온도와 압력 사이의 관계를 보여주는 식이다. 1000hPa 기압고도 $P_0$에서 온도가 $T_0$였던 기체를, 건조단열과정을 따라 강제 상승시켜 어떤 기압고도 $P$에서 온도 $T$가 되었다고 하자. (7) 식을 변수분리하여 이 조건에 따라 양변을 적분하면:

${{dT} \over T} = {R \over c_{p, d}}{{dp} \over p}$

$\int_{T_0}^{T}{{dT} \over T} = \int_{P_0}^{P}{R \over c_{p, d}}{{dp} \over p}$

$[ln T]_{T_0}^{T} = {R \over c_{p, d}}[ln p]_{P_0}^{P}$

$ln({T \over T_0}) = {R \over c_{p, d}}ln({P \over P_0}) = ln(({P \over P_0}^{R \over {c_{p, d}}})$

${T \over T_0} = ({P \over P_0})^{R \over {c_{p, d}}}$

$\therefore T_{0} = T ({P_0 \over P})^{R \over c_{p, d}}$

일반적인 대기과학 교과서에는, 온위 $T_0$를 $\theta$로 표시하고, 건조 대기에 의한 ${R \over c_{p, d}}$를 상수 $k$로 표시하며, 기압은 1hPa 단위로 사용하여 위 공식을 다음과 같이 표현한다(사실 기압은 비율만 수식에서 이용되고 있으므로, 기압 단위는 무엇을 사용해도 무방하다).

$\theta = T({1000 \over P})^k$ (그 공기의 온위 $\theta$, 공기의 기압 $P$ (보통 hPa 단위), 공기의 온도 $T$)

푸아송 방정식.

위와 같은 임의의 공기를 1000hPa 고도로 건조 단열 과정을 통해 옮겼을 때의 온도인 온위를 구하는 수식을, 푸아송 방정식이라고 한다.

이 때, 위 푸아송 방정식에서 상수 $k$의 값은 건조 공기에 대한 $c_p$값 $c_{p, d} = 1004.59 J/kg K$을 이용하면 다음과 같이 구할 수 있다.

$k = {R_{d} \over c_{p, d}}$$ = {{R^*} \over {M_{w} c_{p, d}}} = $${{(8.314 J/mol K) } \over {(28.996 \times 10^{-3} kg/mol)(1004.59 J/kg K)}} = 0.2854$

푸아송 방정식에서의 k값.

참고 문헌

• “[서울 기상센터 Weather Center of Seoul] [기상학] 온위 및 등온위면 분석: 푸아송 방정식 유도하기” – 네이버 블로그, KS서울날씨청, https://m.blog.naver.com/jungjinkim97/221932109421
• “단열과정, 포아송 방정식, 온위, 대기 안정도 판별(대기열역학)” – 네이버 블로그, 리딩웨더, https://m.blog.naver.com/PostView.nhn?blogId=choisignal97&logNo=221794748273&isFromSearchAddView=true
• “열역학 법칙, 2. 열역학 제1법칙 – 에너지 보존 법칙” – 나무위키, https://namu.wiki/w/%EC%97%B4%EC%97%AD%ED%95%99%20%EB%B2%95%EC%B9%99
• “화학적 일, 압력-부피 일, PV-Work” – 티스토리 블로그, 좋은 습관, https://ywpop.tistory.com/5281
• “[자격증] 기상감정기사 필기: 1과목 일반기상학 (대기열역학)” – 티스토리 블로그, shlee1990, https://shlee1990.tistory.com/113
• “정역학적 평형” – 위키백과, 우리 모두의 백과사전, https://ko.wikipedia.org/wiki/%EC%A0%95%EC%97%AD%ED%95%99%EC%A0%81_%ED%8F%89%ED%98%95
• “[대기] 열역학 제1법칙 + 온위” – 네이버 블로그, NOZ의 꿈꾸는 나무, https://blog.naver.com/tnehf18/220504472730
• “대기의 구성성분” – ZUM 학습백과, http://study.zum.com/book/11932